Classification#
Overview#
In classification problems, the output space consists of a set of \(C\) labels, which are referred to as classes. These labels form a set denoted as \(\mathcal{Y} = \{1, 2, \ldots, C\}\). The goal in such problem is to predict the correct label for a given input, a task widely known as pattern recognition.
In cases where there are only two possible classes, the labels are typically represented as \(y \in \{0, 1\}\) or \(y \in \{-1, +1\}\). This specific type of classification is called binary classification.
Iris Flowers#
As an example of a classification task, consider classifying Iris flowers into one of three subspecies: Setosa, Versicolor, and Virginica. The image below illustrates an example from each class.

Three types of Iris flowers: Setosa (left), Versicolor (center), and Virginica (right).
The features in the Iris dataset are: sepal length, sepal width, petal length, and petal width. These features are used to classify the flowers into one of three subspecies: Setosa, Versicolor, or Virginica.
The following code demonstrates how to load the Iris dataset using the sklearn library:
from sklearn import datasets
# Load the Iris dataset
iris = datasets.load_iris()
print(type(iris)) # Print the type of the dataset object
print(iris.feature_names) # Print the names of the dataset's features
print(iris.target_names) # Print the names of the target classes
<class 'sklearn.utils._bunch.Bunch'>
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
['setosa' 'versicolor' 'virginica']
The Iris dataset is a collection of 150 labeled examples of Iris flowers, 50 of each type, described by these 4 features.
import pandas as pd
import numpy as np
# Extract feature data (X) and target labels (y) from the Iris dataset
# Features: Sepal length, sepal width, petal length, petal width
X = iris.data
# Target labels: Encoded as integers (0 = Setosa, 1 = Versicolor, 2 = Virginica)
y = iris.target
# Convert the feature data and target labels into a Pandas DataFrame
df = pd.DataFrame(
data=X, columns=iris.feature_names
) # Create a DataFrame with feature names as column headers
# Display the first few rows of the DataFrame to verify its structure and content
df.head() # Returns the first 5 rows, including features
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | |
|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 |
# Add a new column for human-readable class labels using the target names
# Map the numerical target labels (0, 1, 2) to their corresponding class names (Setosa, Versicolor, Virginica)
df["label"] = pd.Series(iris.target_names[y], dtype="category")
# Display the first few rows of the DataFrame to verify its structure and content
df.head() # Returns the first 5 rows, including features and their corresponding class labels
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | label | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
For tabular data with a small number of features, it is common to make a pair plot, in which panel \((i, j)\) shows a scatter plot of variables \(i\) and \(j\), and the diagonal entries \((i,i)\) show the marginal density of variable \(i\).
import seaborn as sns
import matplotlib.pyplot as plt
# Define a custom color palette to match the colors used in decision tree visualizations
# The keys are the class names (labels), and the values are the colors assigned to each class
palette = {
"setosa": "orange", # Setosa class will be represented in orange
"versicolor": "green", # Versicolor class will be represented in green
"virginica": "purple", # Virginica class will be represented in purple
}
# Create a pair plot using Seaborn to visualize pairwise relationships between features
# - `df`: The DataFrame containing the Iris dataset
# - `vars`: Specifies the columns to use for the pair plot; in this case, the first 4 feature columns
# - `hue`: Groups data points by the "label" column, which corresponds to the class labels
# - `palette`: Applies the custom color mapping defined above for the classes
g = sns.pairplot(df, vars=df.columns[0:4], hue="label", palette=palette)
# Display the resulting plot
plt.show()
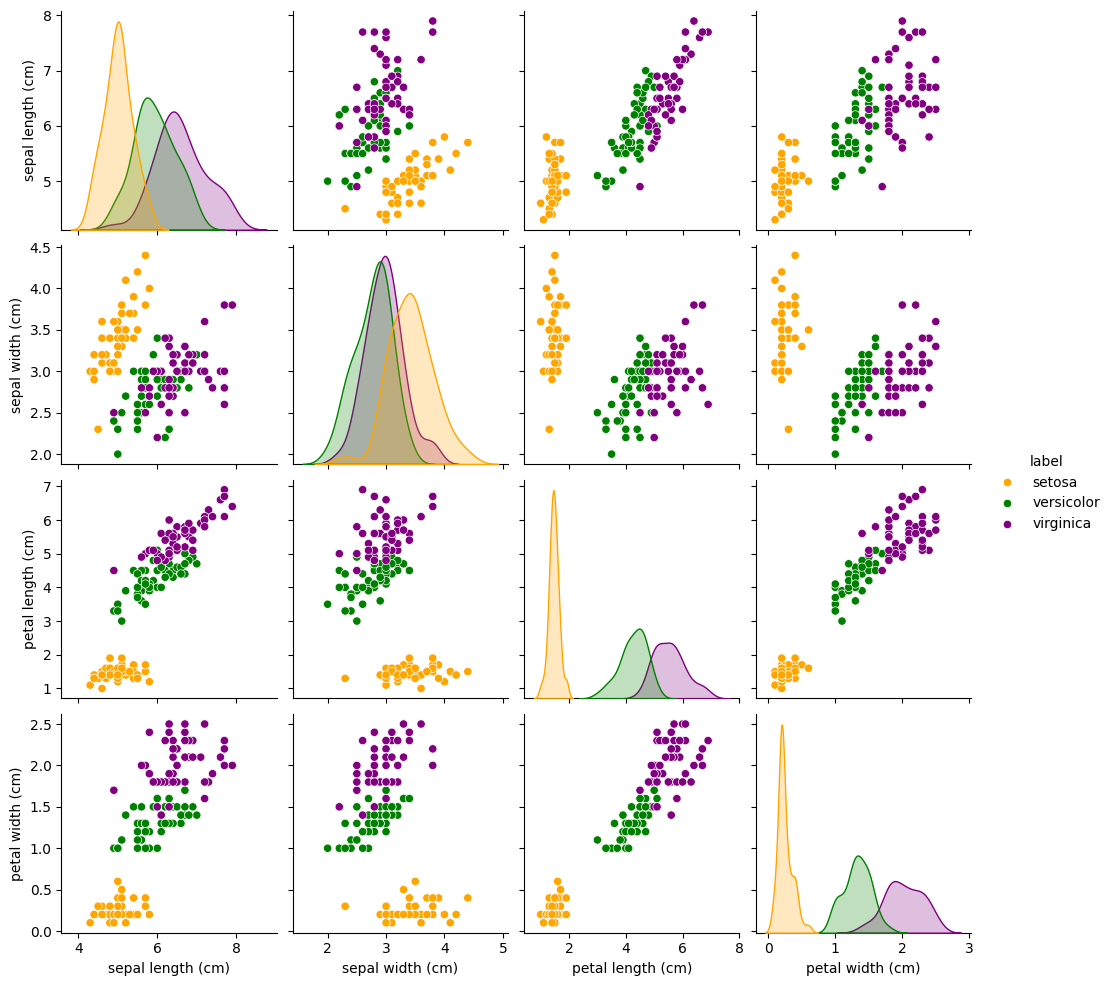
The figure above demonstrates that Iris setosa is easily distinguishable due to its unique feature patterns. However, classifying Iris versicolor and Iris virginica is more difficult because their feature spaces overlap.
Standardization#
Standardization is a preprocessing technique that rescales the features so that they have the properties of a standard normal distribution with a mean of 0 and a standard deviation of 1. This is important in machine learning because it ensures that the features are on a similar scale, preventing some features from dominating the learning process simply because they have larger magnitudes.
The StandardScaler in scikit-learn works by calculating the mean and standard deviation of each feature in the training set and then transforming the data based on these statistics. The formula for standardization is:
The purpose of standardization is to make the features of the dataset comparable and to ensure that they all contribute equally to the model training. It is particularly important when working with algorithms that are sensitive to the scale of the input features, such as gradient-based optimization algorithms used in neural networks.
from sklearn.preprocessing import StandardScaler
# Standardize the features
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# Convert to pandas dataframe
df_scaled = pd.DataFrame(data=X_scaled, columns=iris.feature_names)
df_scaled["label"] = pd.Series(iris.target_names[y], dtype="category")
df_scaled.head()
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | label | |
|---|---|---|---|---|---|
| 0 | -0.900681 | 1.019004 | -1.340227 | -1.315444 | setosa |
| 1 | -1.143017 | -0.131979 | -1.340227 | -1.315444 | setosa |
| 2 | -1.385353 | 0.328414 | -1.397064 | -1.315444 | setosa |
| 3 | -1.506521 | 0.098217 | -1.283389 | -1.315444 | setosa |
| 4 | -1.021849 | 1.249201 | -1.340227 | -1.315444 | setosa |
Splitting Dataset#
To evaluate a classification model effectively, we divide the dataset into two subsets:
Training Set: Used to train the model.
Testing (or Validation) Set: Used to evaluate the model’s performance on unseen data.
This ensures that the model’s performance is measured accurately and prevents overfitting. We’ll use the train_test_split function from scikit-learn to achieve this.
from sklearn.model_selection import train_test_split # For splitting the dataset
from sklearn.naive_bayes import GaussianNB # A classification algorithm (Naive Bayes)
from sklearn.metrics import accuracy_score # To measure the model's performance
# Split the data into training and testing sets
# - X: Feature matrix (sepal/petal dimensions for each Iris sample)
# - y: Target labels (numerical representation of Iris species)
# - test_size=0.2: 20% of the data is reserved for testing, and 80% for training
# - random_state=42: Ensures reproducibility by using a fixed seed for randomness
X_train, X_test, y_train, y_test = train_test_split(
X_scaled, y, test_size=0.2, random_state=42
)
# The train_test_split function performs:
# - Random shuffling of the dataset.
# - Division of data into two parts: training set (X_train, y_train) and testing set (X_test, y_test).
# - A specified proportion for the split (e.g., 80% training, 20% testing).
# Print the shapes of the resulting datasets for verification
print(f"Training set size: {X_train.shape[0]} samples")
print(f"Testing set size: {X_test.shape[0]} samples")
Training set size: 120 samples
Testing set size: 30 samples
Naive Bayes Classifier#
The Naive Bayes method is a probabilistic classifier based on Bayes’ Theorem. It assumes that features are independent given the class label. Since the Iris dataset consists of continuous, real-valued features, we use the Gaussian Naive Bayes classifier, which assumes the feature values are normally distributed.
# Import necessary libraries
from sklearn.naive_bayes import GaussianNB # Gaussian Naive Bayes classifier
from sklearn.metrics import accuracy_score # To evaluate model accuracy
# Train a Gaussian Naive Bayes classifier
nb_classifier = GaussianNB() # Initialize the Gaussian Naive Bayes classifier
# Fit the classifier to the training data
# - X_train: Feature matrix for training
# - y_train: Target labels for training
nb_classifier.fit(X_train, y_train)
# Evaluate the model on the testing set
# - X_test: Feature matrix for testing
# - y_test: Target labels for testing
y_pred = nb_classifier.predict(X_test) # Predict the class labels for the test set
# Calculate the accuracy of the model
accuracy = accuracy_score(y_test, y_pred) # Proportion of correct predictions
print(f"Accuracy: {accuracy * 100:.2f}%") # Print accuracy as a percentage
Accuracy: 100.00%
We’ll train the Gaussian Naive Bayes classifier on the Iris dataset, evaluate its performance using the training and testing sets, and then use 5-fold cross-validation to assess the model’s accuracy across different splits of the dataset.
# Create a Naive Bayes classifier (Gaussian Naive Bayes for this example)
from sklearn.model_selection import cross_val_score
# Perform 5-fold cross-validation to evaluate the model's performance
# - `cv=5`: Specifies 5-fold cross-validation
cv_scores = cross_val_score(nb_classifier, X_scaled, y, cv=5)
# Print cross-validation scores for each fold
print("Cross-validation scores:", cv_scores)
# Calculate and print the mean accuracy from cross-validation
mean_accuracy = np.mean(cv_scores) # Average accuracy across all folds
print("Mean accuracy:", mean_accuracy)
Cross-validation scores: [0.93333333 0.96666667 0.93333333 0.93333333 1. ]
Mean accuracy: 0.9533333333333334
Support Vector Machine (SVM) Classifier#
Support Vector Machines (SVMs) are powerful classification models that find the optimal hyperplane to separate data points in a feature space. SVMs are particularly effective for binary classification, but they can also handle multi-class problems (like the Iris dataset) using extensions like one-vs-one or one-vs-rest strategies.Let’s try the Naive Bayes method to classify the Iris flowers.
Understanding Kernels in SVMs#
Kernels are mathematical functions that transform data into a higher-dimensional space where a linear hyperplane can separate classes. The choice of kernel plays a critical role in the SVM’s ability to handle different types of data:
Linear Kernel: Suitable for linearly separable data. It finds a straight hyperplane to separate the classes.
Polynomial Kernel: Useful when the data requires a polynomial decision boundary.
Radial Basis Function (RBF) Kernel (default): Often a good choice for non-linear data as it maps data to an infinite-dimensional space.
Sigmoid Kernel: Can handle sigmoid-like data distributions but is less commonly used.
The choice of kernel depends on the nature of the data and the problem we are trying to solve. It’s often a good idea to experiment with different kernels to find the one that works best for your specific dataset.
For this example, we use the linear kernel, as it is computationally efficient and works well with the Iris dataset.
from sklearn.svm import SVC # Support Vector Classifier (SVM implementation)
from sklearn.metrics import accuracy_score # For evaluating the model's accuracy
# Initialize the SVM classifier
# - `kernel="linear"`: Specifies that we are using a linear kernel for this example
svm_classifier_linear = SVC(kernel="linear")
# Train the SVM model on the training data
# - `X_train`: Feature matrix for training
# - `y_train`: Target labels for training
svm_classifier_linear.fit(X_train, y_train)
# Evaluate the trained model on the testing set
# - `X_test`: Feature matrix for testing
# - `y_test`: True target labels for testing
y_pred = svm_classifier_linear.predict(X_test) # Predict class labels for the test set
# Calculate the model's accuracy
accuracy = accuracy_score(y_test, y_pred) # Proportion of correct predictions
print(f"Accuracy: {accuracy * 100:.2f}%") # Print accuracy as a percentage
Accuracy: 96.67%
Using 5-Fold Cross-Validation#
We will use 5-fold cross-validation to evaluate the accuracy of our SVM classifier. This approach divides our dataset into five subsets, trains the model on four subsets, and tests it on the remaining subset, repeating this process five times. This method helps us get a reliable estimate of the model’s performance.
from sklearn.model_selection import KFold, cross_val_score
# Define the cross-validation method. We are using 5-fold cross-validation.
# - `n_splits=5` specifies the number of folds.
# - `shuffle=True` ensures that the data is shuffled before splitting into folds, which helps in achieving better generalization.
# - `random_state=42` sets a fixed random seed for reproducibility, so that we get the same data splits every time we run the code.
kf = KFold(n_splits=5, shuffle=True, random_state=42)
# Perform 5-fold cross-validation
# - `svm_classifier` is our model (assumed to be predefined).
# - `X` is the feature matrix (assumed to be predefined).
# - `y` is the target vector (assumed to be predefined).
# - `cv=kf` uses the KFold object we defined as the cross-validation strategy.
cv_scores = cross_val_score(svm_classifier_linear, X_scaled, y, cv=kf)
# Step 4: Print the cross-validation scores for each fold
print("Cross-validation scores:", cv_scores)
# Step 4: Calculate and print the mean accuracy
# - We use `np.mean` to compute the average of the cross-validation scores.
mean_accuracy = np.mean(cv_scores)
print("Mean accuracy:", mean_accuracy)
Cross-validation scores: [0.96666667 0.96666667 0.96666667 0.96666667 1. ]
Mean accuracy: 0.9733333333333334
We want to evaluate the performance of the default kernel, Radial Basis Function (RBF), for a Support Vector Classifier (SVC) using 5-fold cross-validation on the Iris dataset and compare it with the linear kernel.
from sklearn.svm import SVC
from sklearn.model_selection import cross_val_score, KFold
# Define the cross-validation method using 5-fold cross-validation
# - We reuse `kf` from the previous code block for consistency.
kf = KFold(n_splits=5, shuffle=True, random_state=42)
# Create an instance of the classifier
# - `SVC()` creates a Support Vector Classifier with the default RBF kernel.
svm_classifier_rbf = SVC()
# Perform cross-validation and calculate the scores
# - `classifier` is the model we want to evaluate.
# - `X` is the feature matrix (assumed to be predefined).
# - `y` is the target vector (assumed to be predefined).
# - `cv=kf` uses the KFold object we defined as the cross-validation strategy.
# - `scoring="accuracy"` specifies that we want to evaluate the model based on accuracy.
scores = cross_val_score(svm_classifier_rbf, X_scaled, y, cv=kf, scoring="accuracy")
# Print the cross-validation scores for each fold
print("Cross-validation scores:", scores)
# Calculate and print the mean accuracy
# - We use `np.mean` to compute the average of the cross-validation scores.
mean_accuracy = np.mean(scores)
print("Mean accuracy:", mean_accuracy)
Cross-validation scores: [1. 0.96666667 0.96666667 0.93333333 0.96666667]
Mean accuracy: 0.9666666666666668
For this Iris dataset, the linear kernel works better than the RBF kernel.
Neural Networks#
MLPClassifier stands for Multi-Layer Perceptron Classifier. It is a type of artificial neural network-based classification algorithm. The term “multi-layer perceptron” refers to the architecture of the network, which consists of multiple layers of nodes (neurons) organized in a feedforward manner.
The MLPClassifier in scikit-learn has several important parameters that allow you to customize the architecture and behavior of the neural network. Here are some key parameters:
hidden_layer_sizes (default=(100,)): This parameter defines the architecture of the neural network. It is a tuple where each element represents the number of neurons in the corresponding hidden layer. For example, hidden_layer_sizes=(10, 5) defines a network with two hidden layers, the first with 10 neurons and the second with 5.
activation (default=‘relu’): Activation function for the hidden layers. Common choices include ‘relu’ (Rectified Linear Unit), ‘logistic’ (sigmoid), and ‘tanh’ (hyperbolic tangent).
solver (default=‘adam’): Optimization algorithm to use. Common choices include ‘sgd’ (stochastic gradient descent), ‘adam’ (a popular variant of gradient descent), and ‘lbfgs’ (a quasi-Newton method).
learning_rate_init (default=0.001): The initial learning rate. It controls the step size in updating the weights.
max_iter (default=200): Maximum number of iterations. The solver iterates until convergence (determined by the tol parameter) or until this number of iterations is reached.
random_state (default=None): Seed used by the random number generator.
tol (default=1e-4): Tolerance for the optimization. If the change in the objective function is smaller than this value, the optimization will be considered as converged.
verbose: If set to True, it prints progress messages to the console during training.
These are just some of the key parameters. Depending on your specific use case, you may also want to explore other parameters provided by the MLPClassifier class. It’s often beneficial to experiment with different parameter values and architectures to find the combination that works best for your particular dataset and problem.
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import accuracy_score, classification_report
# Create a neural network classifier using scikit-learn's MLPClassifier
mlp = MLPClassifier(
hidden_layer_sizes=(10,),
max_iter=1000,
random_state=42,
solver="sgd",
verbose=1,
tol=1e-4,
learning_rate_init=0.1,
)
# Fit the model to the training data
mlp.fit(X_train, y_train)
# Evaluate the model on the test set
accuracy = mlp.score(X_test, y_test)
print(f"Accuracy on the test set: {accuracy * 100:.2f}")
# Evaluate the performance
y_pred = mlp.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy * 100:.2f}")
# Display classification report
print("Classification Report:\n", classification_report(y_test, y_pred))
Iteration 1, loss = 1.36714411
Iteration 2, loss = 1.18921901
Iteration 3, loss = 1.00875630
Iteration 4, loss = 0.85367491
Iteration 5, loss = 0.72641469
Iteration 6, loss = 0.62117297
Iteration 7, loss = 0.53514402
Iteration 8, loss = 0.46618582
Iteration 9, loss = 0.41118992
Iteration 10, loss = 0.36897772
Iteration 11, loss = 0.33749092
Iteration 12, loss = 0.31376203
Iteration 13, loss = 0.29489437
Iteration 14, loss = 0.27855658
Iteration 15, loss = 0.26350557
Iteration 16, loss = 0.24911145
Iteration 17, loss = 0.23527230
Iteration 18, loss = 0.22198951
Iteration 19, loss = 0.20918275
Iteration 20, loss = 0.19679826
Iteration 21, loss = 0.18482787
Iteration 22, loss = 0.17333673
Iteration 23, loss = 0.16244474
Iteration 24, loss = 0.15226559
Iteration 25, loss = 0.14287097
Iteration 26, loss = 0.13429254
Iteration 27, loss = 0.12654158
Iteration 28, loss = 0.11960936
Iteration 29, loss = 0.11344815
Iteration 30, loss = 0.10800310
Iteration 31, loss = 0.10322739
Iteration 32, loss = 0.09902800
Iteration 33, loss = 0.09533389
Iteration 34, loss = 0.09206149
Iteration 35, loss = 0.08915355
Iteration 36, loss = 0.08651164
Iteration 37, loss = 0.08410219
Iteration 38, loss = 0.08189085
Iteration 39, loss = 0.07984823
Iteration 40, loss = 0.07795653
Iteration 41, loss = 0.07620230
Iteration 42, loss = 0.07457171
Iteration 43, loss = 0.07306074
Iteration 44, loss = 0.07166124
Iteration 45, loss = 0.07036636
Iteration 46, loss = 0.06917159
Iteration 47, loss = 0.06807199
Iteration 48, loss = 0.06706208
Iteration 49, loss = 0.06613767
Iteration 50, loss = 0.06529104
Iteration 51, loss = 0.06451675
Iteration 52, loss = 0.06380757
Iteration 53, loss = 0.06315650
Iteration 54, loss = 0.06255613
Iteration 55, loss = 0.06200054
Iteration 56, loss = 0.06148436
Iteration 57, loss = 0.06100282
Iteration 58, loss = 0.06055187
Iteration 59, loss = 0.06012807
Iteration 60, loss = 0.05972813
Iteration 61, loss = 0.05934928
Iteration 62, loss = 0.05898944
Iteration 63, loss = 0.05864686
Iteration 64, loss = 0.05832015
Iteration 65, loss = 0.05800815
Iteration 66, loss = 0.05771022
Iteration 67, loss = 0.05742552
Iteration 68, loss = 0.05715307
Iteration 69, loss = 0.05689219
Iteration 70, loss = 0.05664224
Iteration 71, loss = 0.05640260
Iteration 72, loss = 0.05617264
Iteration 73, loss = 0.05595186
Iteration 74, loss = 0.05573982
Iteration 75, loss = 0.05553669
Iteration 76, loss = 0.05534131
Iteration 77, loss = 0.05515299
Iteration 78, loss = 0.05497126
Iteration 79, loss = 0.05479565
Iteration 80, loss = 0.05462579
Iteration 81, loss = 0.05446128
Iteration 82, loss = 0.05430176
Iteration 83, loss = 0.05414694
Iteration 84, loss = 0.05399654
Iteration 85, loss = 0.05385031
Iteration 86, loss = 0.05370834
Iteration 87, loss = 0.05357062
Iteration 88, loss = 0.05343657
Iteration 89, loss = 0.05330598
Iteration 90, loss = 0.05317868
Iteration 91, loss = 0.05305452
Iteration 92, loss = 0.05293338
Iteration 93, loss = 0.05281512
Iteration 94, loss = 0.05269964
Iteration 95, loss = 0.05258683
Iteration 96, loss = 0.05247945
Iteration 97, loss = 0.05238325
Iteration 98, loss = 0.05228941
Iteration 99, loss = 0.05219785
Iteration 100, loss = 0.05210848
Iteration 101, loss = 0.05202121
Iteration 102, loss = 0.05193597
Iteration 103, loss = 0.05185268
Iteration 104, loss = 0.05177125
Iteration 105, loss = 0.05169163
Iteration 106, loss = 0.05161374
Iteration 107, loss = 0.05153753
Training loss did not improve more than tol=0.000100 for 10 consecutive epochs. Stopping.
Accuracy on the test set: 100.00
Accuracy: 100.00
Classification Report:
precision recall f1-score support
0 1.00 1.00 1.00 10
1 1.00 1.00 1.00 9
2 1.00 1.00 1.00 11
accuracy 1.00 30
macro avg 1.00 1.00 1.00 30
weighted avg 1.00 1.00 1.00 30
Pipeline#
In scikit-learn, a Pipeline is a way to streamline a lot of the routine processes, especially in the context of feature preprocessing and model building. It sequentially applies a list of transforms and a final estimator. Intermediate steps of the pipeline must be transformers (i.e., they must implement the fit and transform methods), while the final estimator only needs to implement the fit method.
The main purpose of a Pipeline is to assemble several steps that can be cross-validated together while setting different parameters. This ensures that each step in the process is applied in the correct order.
Here’s a simple example using a pipeline with StandardScaler and MLPClassifier:
from sklearn.pipeline import make_pipeline
# Create a pipeline with StandardScaler and MLPClassifier
pipeline = make_pipeline(
StandardScaler(),
MLPClassifier(hidden_layer_sizes=(10,), max_iter=1000, random_state=42),
)
# Fit the pipeline on the training data
pipeline.fit(X_train, y_train)
# Predict using the pipeline
y_pred = pipeline.predict(X_test)
print(y_pred)
print(y_test)
[1 0 2 1 1 0 1 2 1 1 2 0 0 0 0 1 2 1 1 2 0 2 0 2 2 2 2 2 0 0]
[1 0 2 1 1 0 1 2 1 1 2 0 0 0 0 1 2 1 1 2 0 2 0 2 2 2 2 2 0 0]
We want to use 5-fold cross-validation to find accuracy scores and their average.
from sklearn.model_selection import cross_val_score
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline
# Create an MLPClassifier and a pipeline with StandardScaler
pipeline = make_pipeline(StandardScaler(), mlp)
# Perform 5-fold cross-validation
cv_scores = cross_val_score(pipeline, X, y, cv=5)
# Display the cross-validation scores
print("Cross-validation scores:", cv_scores)
print(f"Mean accuracy: {cv_scores.mean():.2f}")
Iteration 1, loss = 1.36430638
Iteration 2, loss = 1.18638437
Iteration 3, loss = 1.00430655
Iteration 4, loss = 0.84704254
Iteration 5, loss = 0.71719051
Iteration 6, loss = 0.61047342
Iteration 7, loss = 0.52313618
Iteration 8, loss = 0.45239689
Iteration 9, loss = 0.39527744
Iteration 10, loss = 0.35048384
Iteration 11, loss = 0.31668698
Iteration 12, loss = 0.29166899
Iteration 13, loss = 0.27259234
Iteration 14, loss = 0.25686986
Iteration 15, loss = 0.24287902
Iteration 16, loss = 0.23014230
Iteration 17, loss = 0.21853451
Iteration 18, loss = 0.20789177
Iteration 19, loss = 0.19811174
Iteration 20, loss = 0.18896397
Iteration 21, loss = 0.18024311
Iteration 22, loss = 0.17184486
Iteration 23, loss = 0.16375180
Iteration 24, loss = 0.15599896
Iteration 25, loss = 0.14862289
Iteration 26, loss = 0.14166167
Iteration 27, loss = 0.13511271
Iteration 28, loss = 0.12897770
Iteration 29, loss = 0.12326143
Iteration 30, loss = 0.11797185
Iteration 31, loss = 0.11312110
Iteration 32, loss = 0.10870332
Iteration 33, loss = 0.10469876
Iteration 34, loss = 0.10108286
Iteration 35, loss = 0.09782786
Iteration 36, loss = 0.09490579
Iteration 37, loss = 0.09228393
Iteration 38, loss = 0.08993143
Iteration 39, loss = 0.08781899
Iteration 40, loss = 0.08591733
Iteration 41, loss = 0.08419727
Iteration 42, loss = 0.08263495
Iteration 43, loss = 0.08120052
Iteration 44, loss = 0.07987413
Iteration 45, loss = 0.07863941
Iteration 46, loss = 0.07748606
Iteration 47, loss = 0.07640092
Iteration 48, loss = 0.07537587
Iteration 49, loss = 0.07440530
Iteration 50, loss = 0.07348518
Iteration 51, loss = 0.07261285
Iteration 52, loss = 0.07178931
Iteration 53, loss = 0.07101067
Iteration 54, loss = 0.07027554
Iteration 55, loss = 0.06958191
Iteration 56, loss = 0.06893039
Iteration 57, loss = 0.06831634
Iteration 58, loss = 0.06773775
Iteration 59, loss = 0.06719259
Iteration 60, loss = 0.06667822
Iteration 61, loss = 0.06619204
Iteration 62, loss = 0.06573166
Iteration 63, loss = 0.06529465
Iteration 64, loss = 0.06487849
Iteration 65, loss = 0.06448098
Iteration 66, loss = 0.06410039
Iteration 67, loss = 0.06373504
Iteration 68, loss = 0.06338346
Iteration 69, loss = 0.06304531
Iteration 70, loss = 0.06271903
Iteration 71, loss = 0.06240344
Iteration 72, loss = 0.06209786
Iteration 73, loss = 0.06180234
Iteration 74, loss = 0.06151588
Iteration 75, loss = 0.06123802
Iteration 76, loss = 0.06096847
Iteration 77, loss = 0.06070699
Iteration 78, loss = 0.06045327
Iteration 79, loss = 0.06020740
Iteration 80, loss = 0.05996891
Iteration 81, loss = 0.05973709
Iteration 82, loss = 0.05951163
Iteration 83, loss = 0.05930208
Iteration 84, loss = 0.05910706
Iteration 85, loss = 0.05891756
Iteration 86, loss = 0.05873335
Iteration 87, loss = 0.05855415
Iteration 88, loss = 0.05837970
Iteration 89, loss = 0.05820979
Iteration 90, loss = 0.05804423
Iteration 91, loss = 0.05788278
Iteration 92, loss = 0.05772525
Iteration 93, loss = 0.05757147
Iteration 94, loss = 0.05742128
Iteration 95, loss = 0.05727454
Iteration 96, loss = 0.05713111
Iteration 97, loss = 0.05699089
Iteration 98, loss = 0.05685376
Iteration 99, loss = 0.05671961
Iteration 100, loss = 0.05658836
Iteration 101, loss = 0.05645991
Iteration 102, loss = 0.05633419
Iteration 103, loss = 0.05621110
Iteration 104, loss = 0.05609058
Iteration 105, loss = 0.05597255
Iteration 106, loss = 0.05585694
Iteration 107, loss = 0.05574381
Iteration 108, loss = 0.05563297
Iteration 109, loss = 0.05552440
Iteration 110, loss = 0.05541803
Iteration 111, loss = 0.05531375
Iteration 112, loss = 0.05521149
Iteration 113, loss = 0.05511122
Iteration 114, loss = 0.05501287
Iteration 115, loss = 0.05491638
Iteration 116, loss = 0.05482170
Iteration 117, loss = 0.05472879
Iteration 118, loss = 0.05463759
Iteration 119, loss = 0.05454806
Iteration 120, loss = 0.05446017
Iteration 121, loss = 0.05437387
Iteration 122, loss = 0.05428912
Iteration 123, loss = 0.05420588
Iteration 124, loss = 0.05412411
Training loss did not improve more than tol=0.000100 for 10 consecutive epochs. Stopping.
Iteration 1, loss = 1.37053717
Iteration 2, loss = 1.19091642
Iteration 3, loss = 1.00974506
Iteration 4, loss = 0.85708767
Iteration 5, loss = 0.73081847
Iteration 6, loss = 0.62724412
Iteration 7, loss = 0.54077526
Iteration 8, loss = 0.46976021
Iteration 9, loss = 0.41275771
Iteration 10, loss = 0.36769027
Iteration 11, loss = 0.33380578
Iteration 12, loss = 0.30857617
Iteration 13, loss = 0.28910824
Iteration 14, loss = 0.27292356
Iteration 15, loss = 0.25835260
Iteration 16, loss = 0.24469510
Iteration 17, loss = 0.23192846
Iteration 18, loss = 0.21993139
Iteration 19, loss = 0.20849521
Iteration 20, loss = 0.19744082
Iteration 21, loss = 0.18668389
Iteration 22, loss = 0.17619373
Iteration 23, loss = 0.16605006
Iteration 24, loss = 0.15636346
Iteration 25, loss = 0.14723744
Iteration 26, loss = 0.13875282
Iteration 27, loss = 0.13092988
Iteration 28, loss = 0.12379402
Iteration 29, loss = 0.11736141
Iteration 30, loss = 0.11162416
Iteration 31, loss = 0.10657672
Iteration 32, loss = 0.10215249
Iteration 33, loss = 0.09827784
Iteration 34, loss = 0.09488001
Iteration 35, loss = 0.09190627
Iteration 36, loss = 0.08925092
Iteration 37, loss = 0.08686448
Iteration 38, loss = 0.08469719
Iteration 39, loss = 0.08270115
Iteration 40, loss = 0.08085176
Iteration 41, loss = 0.07912199
Iteration 42, loss = 0.07749574
Iteration 43, loss = 0.07596664
Iteration 44, loss = 0.07453222
Iteration 45, loss = 0.07319134
Iteration 46, loss = 0.07194291
Iteration 47, loss = 0.07078518
Iteration 48, loss = 0.06971581
Iteration 49, loss = 0.06873408
Iteration 50, loss = 0.06783480
Iteration 51, loss = 0.06700902
Iteration 52, loss = 0.06625062
Iteration 53, loss = 0.06555383
Iteration 54, loss = 0.06491311
Iteration 55, loss = 0.06432085
Iteration 56, loss = 0.06377137
Iteration 57, loss = 0.06325952
Iteration 58, loss = 0.06278073
Iteration 59, loss = 0.06233155
Iteration 60, loss = 0.06190897
Iteration 61, loss = 0.06150938
Iteration 62, loss = 0.06113047
Iteration 63, loss = 0.06077037
Iteration 64, loss = 0.06042755
Iteration 65, loss = 0.06010076
Iteration 66, loss = 0.05978900
Iteration 67, loss = 0.05949147
Iteration 68, loss = 0.05920753
Iteration 69, loss = 0.05893626
Iteration 70, loss = 0.05867697
Iteration 71, loss = 0.05842901
Iteration 72, loss = 0.05819175
Iteration 73, loss = 0.05796457
Iteration 74, loss = 0.05774683
Iteration 75, loss = 0.05753790
Iteration 76, loss = 0.05733717
Iteration 77, loss = 0.05714407
Iteration 78, loss = 0.05695803
Iteration 79, loss = 0.05677856
Iteration 80, loss = 0.05660518
Iteration 81, loss = 0.05643746
Iteration 82, loss = 0.05627518
Iteration 83, loss = 0.05611797
Iteration 84, loss = 0.05596540
Iteration 85, loss = 0.05581721
Iteration 86, loss = 0.05567315
Iteration 87, loss = 0.05553301
Iteration 88, loss = 0.05539662
Iteration 89, loss = 0.05526380
Iteration 90, loss = 0.05513441
Iteration 91, loss = 0.05500829
Iteration 92, loss = 0.05488531
Iteration 93, loss = 0.05476536
Iteration 94, loss = 0.05464834
Iteration 95, loss = 0.05453414
Iteration 96, loss = 0.05442303
Iteration 97, loss = 0.05431468
Iteration 98, loss = 0.05420884
Iteration 99, loss = 0.05410542
Iteration 100, loss = 0.05400432
Iteration 101, loss = 0.05390544
Iteration 102, loss = 0.05380870
Iteration 103, loss = 0.05371401
Iteration 104, loss = 0.05362128
Iteration 105, loss = 0.05353045
Iteration 106, loss = 0.05344153
Iteration 107, loss = 0.05335442
Iteration 108, loss = 0.05326900
Iteration 109, loss = 0.05318521
Iteration 110, loss = 0.05310300
Iteration 111, loss = 0.05302230
Training loss did not improve more than tol=0.000100 for 10 consecutive epochs. Stopping.
Iteration 1, loss = 1.36441069
Iteration 2, loss = 1.18928975
Iteration 3, loss = 1.01073523
Iteration 4, loss = 0.85269461
Iteration 5, loss = 0.71890050
Iteration 6, loss = 0.61182349
Iteration 7, loss = 0.52463950
Iteration 8, loss = 0.45271891
Iteration 9, loss = 0.39323726
Iteration 10, loss = 0.34631670
Iteration 11, loss = 0.31111222
Iteration 12, loss = 0.28526401
Iteration 13, loss = 0.26554056
Iteration 14, loss = 0.24936608
Iteration 15, loss = 0.23511561
Iteration 16, loss = 0.22195200
Iteration 17, loss = 0.20955486
Iteration 18, loss = 0.19784594
Iteration 19, loss = 0.18667766
Iteration 20, loss = 0.17588505
Iteration 21, loss = 0.16537519
Iteration 22, loss = 0.15512473
Iteration 23, loss = 0.14519038
Iteration 24, loss = 0.13565787
Iteration 25, loss = 0.12663978
Iteration 26, loss = 0.11822399
Iteration 27, loss = 0.11046435
Iteration 28, loss = 0.10339463
Iteration 29, loss = 0.09701325
Iteration 30, loss = 0.09130672
Iteration 31, loss = 0.08624821
Iteration 32, loss = 0.08177146
Iteration 33, loss = 0.07779398
Iteration 34, loss = 0.07432552
Iteration 35, loss = 0.07128922
Iteration 36, loss = 0.06861213
Iteration 37, loss = 0.06625795
Iteration 38, loss = 0.06414392
Iteration 39, loss = 0.06221070
Iteration 40, loss = 0.06042450
Iteration 41, loss = 0.05875940
Iteration 42, loss = 0.05720561
Iteration 43, loss = 0.05574942
Iteration 44, loss = 0.05438351
Iteration 45, loss = 0.05310685
Iteration 46, loss = 0.05191619
Iteration 47, loss = 0.05080816
Iteration 48, loss = 0.04978189
Iteration 49, loss = 0.04883494
Iteration 50, loss = 0.04796359
Iteration 51, loss = 0.04716373
Iteration 52, loss = 0.04643060
Iteration 53, loss = 0.04575906
Iteration 54, loss = 0.04514371
Iteration 55, loss = 0.04457916
Iteration 56, loss = 0.04406010
Iteration 57, loss = 0.04358156
Iteration 58, loss = 0.04313916
Iteration 59, loss = 0.04272847
Iteration 60, loss = 0.04234563
Iteration 61, loss = 0.04198801
Iteration 62, loss = 0.04165201
Iteration 63, loss = 0.04133519
Iteration 64, loss = 0.04103570
Iteration 65, loss = 0.04075198
Iteration 66, loss = 0.04048226
Iteration 67, loss = 0.04022540
Iteration 68, loss = 0.03998043
Iteration 69, loss = 0.03974658
Iteration 70, loss = 0.03952314
Iteration 71, loss = 0.03930986
Iteration 72, loss = 0.03910649
Iteration 73, loss = 0.03891197
Iteration 74, loss = 0.03872588
Iteration 75, loss = 0.03854774
Iteration 76, loss = 0.03837714
Iteration 77, loss = 0.03821369
Iteration 78, loss = 0.03805704
Iteration 79, loss = 0.03790676
Iteration 80, loss = 0.03776249
Iteration 81, loss = 0.03762388
Iteration 82, loss = 0.03749058
Iteration 83, loss = 0.03736227
Iteration 84, loss = 0.03723865
Iteration 85, loss = 0.03711946
Iteration 86, loss = 0.03700441
Iteration 87, loss = 0.03689330
Iteration 88, loss = 0.03678595
Iteration 89, loss = 0.03668210
Iteration 90, loss = 0.03658194
Iteration 91, loss = 0.03648476
Iteration 92, loss = 0.03639041
Iteration 93, loss = 0.03629875
Iteration 94, loss = 0.03620966
Iteration 95, loss = 0.03612344
Iteration 96, loss = 0.03603958
Iteration 97, loss = 0.03595803
Iteration 98, loss = 0.03587869
Iteration 99, loss = 0.03580148
Iteration 100, loss = 0.03572631
Iteration 101, loss = 0.03565327
Training loss did not improve more than tol=0.000100 for 10 consecutive epochs. Stopping.
Iteration 1, loss = 1.36536424
Iteration 2, loss = 1.18934857
Iteration 3, loss = 1.00971561
Iteration 4, loss = 0.85453727
Iteration 5, loss = 0.72698235
Iteration 6, loss = 0.62185733
Iteration 7, loss = 0.53532188
Iteration 8, loss = 0.46445608
Iteration 9, loss = 0.40615461
Iteration 10, loss = 0.36030636
Iteration 11, loss = 0.32557038
Iteration 12, loss = 0.29933856
Iteration 13, loss = 0.27870997
Iteration 14, loss = 0.26121532
Iteration 15, loss = 0.24507580
Iteration 16, loss = 0.22970766
Iteration 17, loss = 0.21517271
Iteration 18, loss = 0.20138770
Iteration 19, loss = 0.18820606
Iteration 20, loss = 0.17555273
Iteration 21, loss = 0.16338346
Iteration 22, loss = 0.15173267
Iteration 23, loss = 0.14070763
Iteration 24, loss = 0.13043045
Iteration 25, loss = 0.12099926
Iteration 26, loss = 0.11243575
Iteration 27, loss = 0.10473194
Iteration 28, loss = 0.09786647
Iteration 29, loss = 0.09181844
Iteration 30, loss = 0.08650151
Iteration 31, loss = 0.08185301
Iteration 32, loss = 0.07781153
Iteration 33, loss = 0.07431630
Iteration 34, loss = 0.07123966
Iteration 35, loss = 0.06849201
Iteration 36, loss = 0.06601492
Iteration 37, loss = 0.06376054
Iteration 38, loss = 0.06168184
Iteration 39, loss = 0.05975035
Iteration 40, loss = 0.05794569
Iteration 41, loss = 0.05625389
Iteration 42, loss = 0.05466633
Iteration 43, loss = 0.05317475
Iteration 44, loss = 0.05177830
Iteration 45, loss = 0.05047714
Iteration 46, loss = 0.04926922
Iteration 47, loss = 0.04814596
Iteration 48, loss = 0.04710344
Iteration 49, loss = 0.04613692
Iteration 50, loss = 0.04524098
Iteration 51, loss = 0.04440973
Iteration 52, loss = 0.04363707
Iteration 53, loss = 0.04291688
Iteration 54, loss = 0.04224315
Iteration 55, loss = 0.04161123
Iteration 56, loss = 0.04101490
Iteration 57, loss = 0.04044969
Iteration 58, loss = 0.03991178
Iteration 59, loss = 0.03939798
Iteration 60, loss = 0.03890586
Iteration 61, loss = 0.03843334
Iteration 62, loss = 0.03797881
Iteration 63, loss = 0.03754110
Iteration 64, loss = 0.03711915
Iteration 65, loss = 0.03671215
Iteration 66, loss = 0.03631942
Iteration 67, loss = 0.03594029
Iteration 68, loss = 0.03557412
Iteration 69, loss = 0.03522029
Iteration 70, loss = 0.03487816
Iteration 71, loss = 0.03454710
Iteration 72, loss = 0.03422629
Iteration 73, loss = 0.03391500
Iteration 74, loss = 0.03361254
Iteration 75, loss = 0.03331826
Iteration 76, loss = 0.03303156
Iteration 77, loss = 0.03275188
Iteration 78, loss = 0.03247874
Iteration 79, loss = 0.03221170
Iteration 80, loss = 0.03195041
Iteration 81, loss = 0.03169452
Iteration 82, loss = 0.03144401
Iteration 83, loss = 0.03119856
Iteration 84, loss = 0.03095783
Iteration 85, loss = 0.03072234
Iteration 86, loss = 0.03049124
Iteration 87, loss = 0.03026437
Iteration 88, loss = 0.03004159
Iteration 89, loss = 0.02982275
Iteration 90, loss = 0.02960788
Iteration 91, loss = 0.02939683
Iteration 92, loss = 0.02918932
Iteration 93, loss = 0.02898524
Iteration 94, loss = 0.02878469
Iteration 95, loss = 0.02859795
Iteration 96, loss = 0.02842043
Iteration 97, loss = 0.02824586
Iteration 98, loss = 0.02807409
Iteration 99, loss = 0.02790504
Iteration 100, loss = 0.02773861
Iteration 101, loss = 0.02757470
Iteration 102, loss = 0.02741323
Iteration 103, loss = 0.02725411
Iteration 104, loss = 0.02709727
Iteration 105, loss = 0.02694251
Iteration 106, loss = 0.02678859
Iteration 107, loss = 0.02663643
Iteration 108, loss = 0.02648605
Iteration 109, loss = 0.02633739
Iteration 110, loss = 0.02619043
Iteration 111, loss = 0.02604515
Iteration 112, loss = 0.02590152
Iteration 113, loss = 0.02575953
Iteration 114, loss = 0.02561915
Iteration 115, loss = 0.02548035
Iteration 116, loss = 0.02534310
Iteration 117, loss = 0.02520738
Iteration 118, loss = 0.02507317
Iteration 119, loss = 0.02494044
Iteration 120, loss = 0.02480917
Iteration 121, loss = 0.02467933
Iteration 122, loss = 0.02455090
Iteration 123, loss = 0.02442385
Iteration 124, loss = 0.02429817
Iteration 125, loss = 0.02417382
Iteration 126, loss = 0.02405079
Iteration 127, loss = 0.02392905
Iteration 128, loss = 0.02380859
Iteration 129, loss = 0.02368937
Iteration 130, loss = 0.02357139
Iteration 131, loss = 0.02345461
Iteration 132, loss = 0.02333902
Iteration 133, loss = 0.02322460
Iteration 134, loss = 0.02311131
Iteration 135, loss = 0.02299915
Iteration 136, loss = 0.02288810
Iteration 137, loss = 0.02277814
Iteration 138, loss = 0.02266925
Iteration 139, loss = 0.02256135
Iteration 140, loss = 0.02245444
Iteration 141, loss = 0.02234854
Iteration 142, loss = 0.02224364
Iteration 143, loss = 0.02213973
Iteration 144, loss = 0.02203694
Iteration 145, loss = 0.02193512
Iteration 146, loss = 0.02183422
Iteration 147, loss = 0.02173426
Iteration 148, loss = 0.02163522
Iteration 149, loss = 0.02153707
Iteration 150, loss = 0.02143981
Iteration 151, loss = 0.02134341
Iteration 152, loss = 0.02124795
Iteration 153, loss = 0.02115335
Iteration 154, loss = 0.02105965
Iteration 155, loss = 0.02096676
Iteration 156, loss = 0.02087467
Iteration 157, loss = 0.02078440
Training loss did not improve more than tol=0.000100 for 10 consecutive epochs. Stopping.
Iteration 1, loss = 1.36797352
Iteration 2, loss = 1.18583880
Iteration 3, loss = 1.00099545
Iteration 4, loss = 0.84157584
Iteration 5, loss = 0.71441066
Iteration 6, loss = 0.61007590
Iteration 7, loss = 0.52421464
Iteration 8, loss = 0.45472091
Iteration 9, loss = 0.40000432
Iteration 10, loss = 0.35872454
Iteration 11, loss = 0.32866051
Iteration 12, loss = 0.30673678
Iteration 13, loss = 0.28971216
Iteration 14, loss = 0.27514503
Iteration 15, loss = 0.26186964
Iteration 16, loss = 0.24922873
Iteration 17, loss = 0.23693466
Iteration 18, loss = 0.22491835
Iteration 19, loss = 0.21319302
Iteration 20, loss = 0.20172623
Iteration 21, loss = 0.19050125
Iteration 22, loss = 0.17960024
Iteration 23, loss = 0.16916073
Iteration 24, loss = 0.15931835
Iteration 25, loss = 0.15017168
Iteration 26, loss = 0.14177807
Iteration 27, loss = 0.13416185
Iteration 28, loss = 0.12732320
Iteration 29, loss = 0.12124065
Iteration 30, loss = 0.11586813
Iteration 31, loss = 0.11114532
Iteration 32, loss = 0.10699965
Iteration 33, loss = 0.10339085
Iteration 34, loss = 0.10018051
Iteration 35, loss = 0.09726082
Iteration 36, loss = 0.09457392
Iteration 37, loss = 0.09207729
Iteration 38, loss = 0.08974217
Iteration 39, loss = 0.08755197
Iteration 40, loss = 0.08550359
Iteration 41, loss = 0.08358075
Iteration 42, loss = 0.08178881
Iteration 43, loss = 0.08012658
Iteration 44, loss = 0.07858657
Iteration 45, loss = 0.07716542
Iteration 46, loss = 0.07585819
Iteration 47, loss = 0.07465588
Iteration 48, loss = 0.07355009
Iteration 49, loss = 0.07253458
Iteration 50, loss = 0.07159825
Iteration 51, loss = 0.07073323
Iteration 52, loss = 0.06993159
Iteration 53, loss = 0.06918554
Iteration 54, loss = 0.06848780
Iteration 55, loss = 0.06783226
Iteration 56, loss = 0.06721382
Iteration 57, loss = 0.06662839
Iteration 58, loss = 0.06607251
Iteration 59, loss = 0.06554347
Iteration 60, loss = 0.06503894
Iteration 61, loss = 0.06455856
Iteration 62, loss = 0.06410071
Iteration 63, loss = 0.06366393
Iteration 64, loss = 0.06324707
Iteration 65, loss = 0.06284906
Iteration 66, loss = 0.06246890
Iteration 67, loss = 0.06210562
Iteration 68, loss = 0.06175820
Iteration 69, loss = 0.06142561
Iteration 70, loss = 0.06110659
Iteration 71, loss = 0.06080099
Iteration 72, loss = 0.06050737
Iteration 73, loss = 0.06022472
Iteration 74, loss = 0.05995219
Iteration 75, loss = 0.05968900
Iteration 76, loss = 0.05943443
Iteration 77, loss = 0.05918800
Iteration 78, loss = 0.05895143
Iteration 79, loss = 0.05872286
Iteration 80, loss = 0.05850101
Iteration 81, loss = 0.05828583
Iteration 82, loss = 0.05807681
Iteration 83, loss = 0.05787376
Iteration 84, loss = 0.05767633
Iteration 85, loss = 0.05748427
Iteration 86, loss = 0.05729735
Iteration 87, loss = 0.05711535
Iteration 88, loss = 0.05693804
Iteration 89, loss = 0.05676677
Iteration 90, loss = 0.05660086
Iteration 91, loss = 0.05643917
Iteration 92, loss = 0.05628149
Iteration 93, loss = 0.05612761
Iteration 94, loss = 0.05597738
Iteration 95, loss = 0.05583063
Iteration 96, loss = 0.05568720
Iteration 97, loss = 0.05554695
Iteration 98, loss = 0.05540974
Iteration 99, loss = 0.05527544
Iteration 100, loss = 0.05515231
Iteration 101, loss = 0.05503668
Iteration 102, loss = 0.05492394
Iteration 103, loss = 0.05481382
Iteration 104, loss = 0.05470615
Iteration 105, loss = 0.05460086
Iteration 106, loss = 0.05449788
Iteration 107, loss = 0.05439711
Iteration 108, loss = 0.05429846
Iteration 109, loss = 0.05420187
Iteration 110, loss = 0.05410728
Iteration 111, loss = 0.05401463
Iteration 112, loss = 0.05392384
Iteration 113, loss = 0.05383487
Iteration 114, loss = 0.05374766
Iteration 115, loss = 0.05366215
Iteration 116, loss = 0.05357829
Iteration 117, loss = 0.05349603
Iteration 118, loss = 0.05341532
Training loss did not improve more than tol=0.000100 for 10 consecutive epochs. Stopping.
Cross-validation scores: [1. 1. 0.93333333 0.93333333 0.96666667]
Mean accuracy: 0.97

